Algorithms. Analysis - Part I

This is a first entry post about algorithms. References to other parts will be added later.

Let's start with identifying why and when algorithms analysis can be used for.

Why do we need algorithms analysis?

Ideally, it is used when we have several approaches/algorithms for solving the same problem. The main goal for us is to find the most performant and cost-effective algorithm. Of course, sometimes you have to balance and understand the context. But, ideally, your algorithm should be performant. We can call algorithm performant when it can be executed comparatively fast utilizing CPU less.

Algorithms analysis means predicting the required resources that algorithm requires. By required resources here we can understand: computation time and memory. Those are things that we are interested in the most. We are not interested which exact CPU or memory is installed, otherwise it will be tricky to have a unified approach for measuring and comparing alogorithms between each other.

The first step in doing the algorithm analysis is to define a model which will be used for the actual analysis. The main purpose of the model is to help us to define the cost of each line. Generally speaking, it could be done like this:

1. Arithmetic operation, assignment etc. will cost 1. Here 1 means that we need only one instruction to calculate/execute the line.
2. Loops such as traverse n elements and execute the instruction will cost n as we are executing it n times.

Example

Let's gain an idea on applying this model to code before we dive into futher details. We are going to use Java, but this is applicatble to any language of preference.

Simple sum

The following example is a fairly simple one. This will allow us to demonstrate and gain understnading how we are going to use the model.

private static void sum() {
  var sum = 0;

  for (var i = 0; i < 10; i++) {
    sum += i;
  }

  System.out.println(sum);
}

Having code above, we can see that each line contains instructions that needs to be executed. Let's go through each line having in mind model which we described above.

private static void sum() {
  // 1. assignment operation. Cost = 1
  var sum = 0;

  // 2. loop. We are looping through 10 element and in this case
  // cost = 10
  for (var i = 0; i < 10; i++) {
    
    // 3. this line contains from 2 statements
    // sum = sum + i 
    // where we are adding first and then we are assigning
    sum += i;
  }

  // 4. standard print. Const = 1
  System.out.println(sum);
}

Having that analysis above, we can calculate the cost of sum() method. Let's calculate total using numbers in code 1, 2, 3, 4:

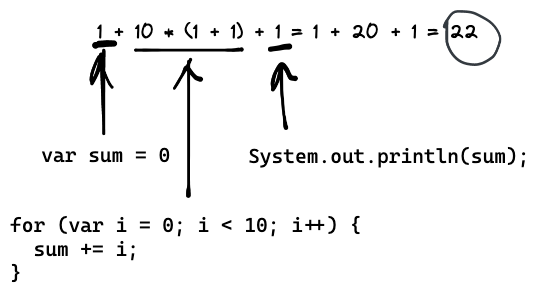
That gives us measurable approach on how to measure the algorithm's runtime. As a next step, let's try to generalize it. The reason for generalization is simple: we need an approach how to measure algorithm's runtime for other cases when loop (for end condition) is unknown. Let's take a look at modified sum method, but right now it will accept an argument n:

private static void sum(int n) {
  // 1. assignment operation. Cost = 1
  var sum = 0;

  // 2. loop. We are looping through 10 element and in this case
  // cost = 10
  for (var i = 0; i < n; i++) {
    
    // 3. this line contains from 2 statements
    // sum = sum + i 
    // where we are adding first and then we are assigning
    sum += i;
  }

  // 4. standard print. Const = 1
  System.out.println(sum);
}

After making this change, we can see how it affects the calculation part:

Here 2n + 2 is the final runtime calculation for this algorithm. For example, if we replace n with 100, then it will be 2*100 + 2 = 202. Executing one instruction or two does not make much difference for us. Basically, we can omit 2 from this experession 2n + 2 → 2n. We can say that the complexity of this algorithm is 2n. But, do we really interested in what is happening inside of the loop having in mind that those expressions have only runtime complexity of 1 for each of the instruction. Taking this into account, we can consider that 2n could be simplified to just n.

Additionally, let's build a graph which will demonstrate the effect of increasing n input size vs. number of operations N.

Doing this analysis we just came to the idea of finding the algorithm's time complexity. Usually, we refer to it like Big O notation (or O(n)).

O(n) – notation that is used to classify algorithms according to how their run time or space requirements grow as the input size grows.

Wiki

Next time we are going to dive deep into Big O notation and start taking a look at other cases with inner loops etc.